Denkwerk: Rekenen met origami

Koen Vervloesem

Logische poorten vormen de basis van elke microprocessor, of die nu in je computer zit, je smartphone of een microcontrollerbordje zoals een Arduino. Zo’n poort heeft één of meer binaire inputs en één output. Met binair bedoelen we dat een waarde 0 of 1 kan zijn, ook wel eens voorgesteld als False of True.

Een voorbeeld is de OR-poort. De output daarvan is 1 als minstens één van de inputs 1 is. Bij de AND-poort is de output dan weer alleen 1 als allebei de inputs 1 zijn. En de NOT-poort heeft maar één input. De uitvoer daarvan is 1 als de input 0 is en omgekeerd. Door al deze (en nog andere) poorten op de juiste manier te combineren, kun je allerlei berekeningen uitvoeren.

Elektronische computers implementeren die logische poorten met behulp van transistoren, die elektronische signalen kunnen schakelen. Uiteraard is dat tegenwoordig enorm geminiaturiseerd: een chip bestaat al snel uit miljarden transistoren. Maar je kunt logische poorten ook op andere manieren implementeren, die niet elektronisch hoeven te zijn. Dan kun je in principe een computer bouwen zonder elektronica.

Papieren poorten

Dat is nu net wat wiskundigen Thomas Hull (http://origametry.net) en Inna Zakharevich (https://pi.math.cornell.edu/~zakh/) deden. In hun artikel “Flat origami is Turing Complete” (https://arxiv.org/abs/2309.07932v2) bewezen ze niet alleen dat je met vlak gevouwen papier alle mogelijke berekeningen kunt uitvoeren, ze construeerden ook logische poorten met origami. Dat begon met het uitdenken van logische poorten én een voorstelling van de bits 0 en 1 in termen van het vouwen van papier.

De beste manier om iets te begrijpen is om het zelf toe te passen, dus ik raad je aan om deze Denkwerk mee te volgen door de logische poorten zelf te vouwen en ze met verschillende inputs uit te proberen. Inna Zakharevich is zo behulpzaam geweest om op haar website vouwpatronen (https://pi.math.cornell.edu/~zakh/crease-patterns.pdf) voor de logische poorten en andere componenten aan te bieden. Druk dit document af, knip ruim rond de patronen een willekeurige vorm uit, en vouw dan volgens het afgedrukte patroon. Elke poort staat vier keer op een pagina afgebeeld, dus door het document één keer te printen, kun je al heel wat experimenteren. Let wel op: print enkelzijdig, zodat je in alle pagina’s kunt knippen.

Een input of output wordt in hun systeem voorgesteld door parallelle vouwlijnen: een ‘berg’ in het midden en links en rechts daarvan een optionele ‘vallei’. In origami zijn de berg en de vallei de twee basisvouwen. We spreken van een berg als je een vouw maakt waardoor de vouwlijn boven het papier aan beide kanten van de vouw staat. We spreken van een vallei als de vouwlijn onder het papier aan beide kanten van de vouw staat. In het systeem van Hull en Zakharevich heeft een input of output nu de waarde FALSE als de plooi naar rechts wordt gevouwen, anders TRUE.

OR-poort

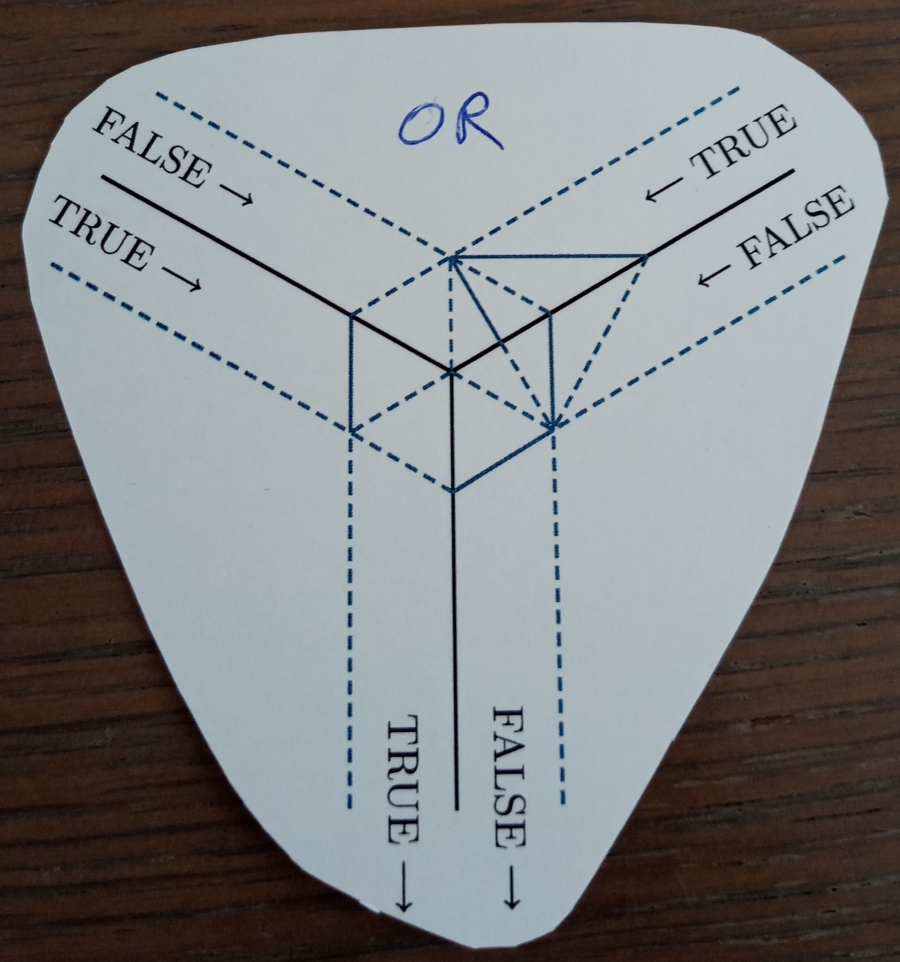
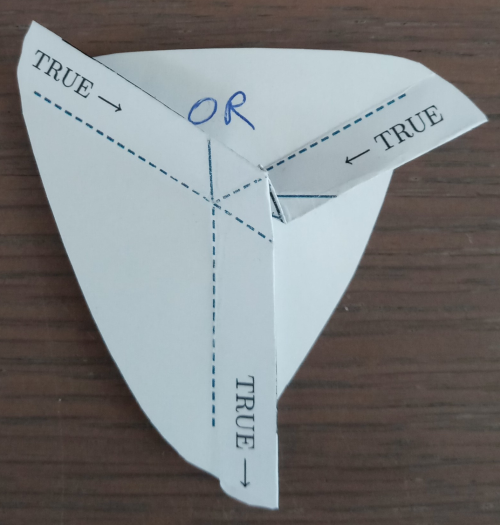
 Een voorbeeld zal dit duidelijk maken. Knip een OR-poort uit. Het maakt niet uit welke vorm, als je maar rond alle lijnen knipt. Je gaat dan bijvoorbeeld een driehoekig papier met afgeronde hoeken hebben (afbeelding 1). Maak nu bij alle volle zwarte en blauwe lijnen een bergvouw, en bij alle blauwe stippellijnen een valleivouw. De lijnen die blauw zijn, wijzen erop dat het van de waarde van een bit afhangt of de lijn gevouwen is of plat ligt. Maar vouw ze dus eerst allemaal. Een liniaal, bankkaart of vouwbeen kan hierbij helpen.

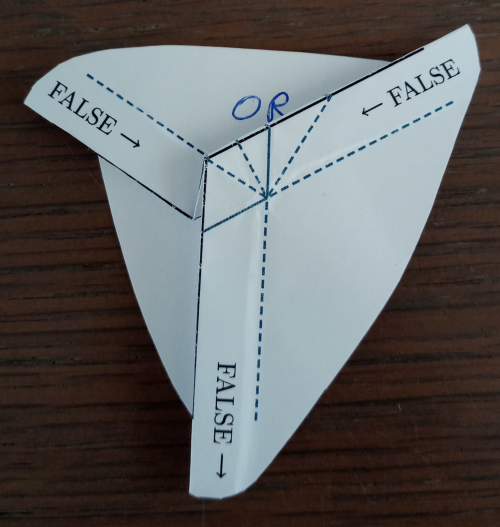1 - Het vouwpatroon van de OR-poort	2 - False OR False geeft False

Bovenaan links en rechts komen de twee inputs. Dit wordt aangeduid met de twee pijlen naar binnen. Onderaan komt de output van de OR-poort, zoals is aangeduid met de twee pijlen naar buiten. De output van een OR-poort is slechts FALSE wanneer de twee inputs FALSE zijn. Vouw dus een van de twee valleivouwen bij beide inputs op zo’n manier dat je bij allebei FALSE ziet (2). Door het complexe samenspel van de berg- en valleivouwen in en rond de zeshoek in het midden forceert die de vouwen onderaan zo dat in de output ook FALSE boven komt te liggen.

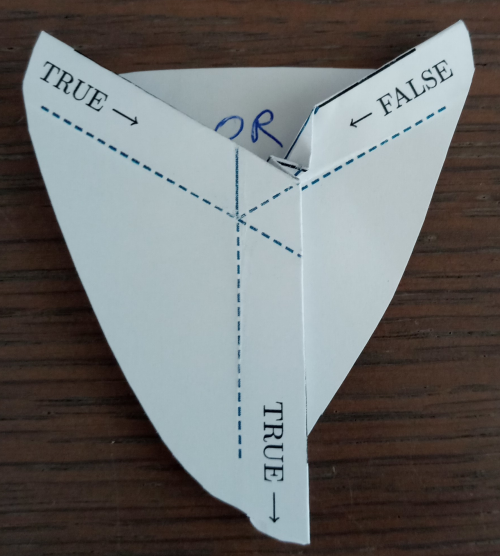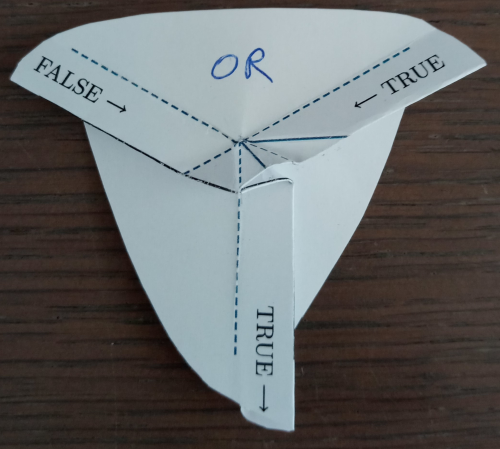
3 - False OR True geeft True	4 - True OR False geeft True

Als je nu de rechter input naar TRUE vouwt, forceert dit de output naar TRUE (3). Vouw je deze input terug naar FALSE en vouw je dan de linker input naar TRUE, dan wordt de output ook naar TRUE geforceerd (4). Vouw je nu beide inputs naar TRUE, dan forceert dit ook de output op TRUE (5). Kortom, als je alle vier de mogelijke combinaties van de twee inputs bekijkt, krijg je als output altijd de waarde van de OR-operatie. We hebben dus een werkende logische OR-poort in papier.

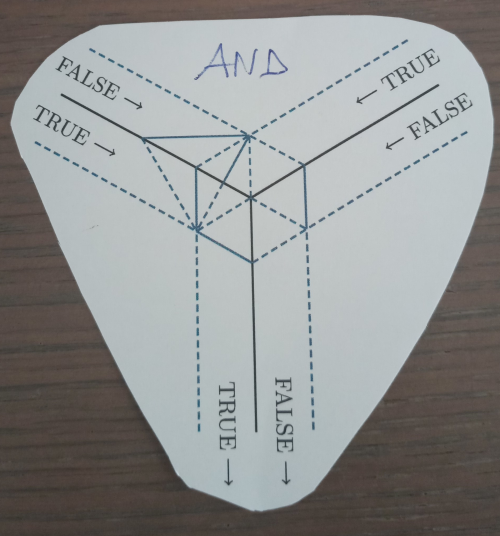5 - True OR True geeft True	6 - Het vouwpatroon van de AND-poort

AND- en NOT-poort

De AND-poort steekt gelijkaardig in elkaar als de OR-poort. Maar nu is de output slechts TRUE wanneer de twee inputs TRUE zijn (6). Knip deze dus ook uit, vouw op de lijnen van het vouwpatroon en probeer eens alle vier de combinaties van inputs uit om te kijken hoe de output telkens naar de juiste waarde wordt geforceerd. Let erop dat alle blauwe lijnen in elke situatie correct worden gevouwen zodat je telkens een volledig vlakke constructie krijgt.

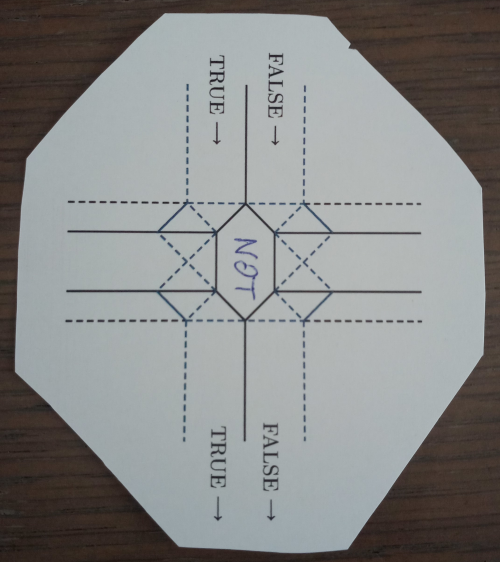
7 - Het vouwpatroon van de NOT-poort	8 - NOT False geeft True

 
De NOT-poort ziet er wat anders uit, omdat die nu eenmaal maar één input heeft (7). Boven vouw je de input naar TRUE of FALSE, en door de constructie van de vouwen in het midden vouwt je output naar FALSE respectievelijk TRUE. Deze poort is wel wat moeilijker te vouwen. In het midden heb je immers een zeskantige draai. Door de input van FALSE naar TRUE te veranderen of andersom, draait de zeshoek in het midden maar liefst 180 graden, waardoor dan uiteindelijk ook de output mee draait (8 en 9).

9 - NOT True geeft False	10 - Het vouwpatroon van de driehoekige draai

 
Complexe logische schakelingen

Hull en Zakharevich hebben zo nog enkele poorten en andere componenten uitgevonden. Die kun je dan in een driehoekig raster aan elkaar koppelen om complexere logische schakelingen te creëren. Als je voor dat koppelen lijnen van richting zou moeten veranderen, bestaan daar ook componenten voor, zoals een zeshoekige en driehoekige draai. Die laatste bijvoorbeeld heeft drie lijnen. Als één ervan als input naar de waarde TRUE vouwt, vouwen de twee andere als outputs naar diezelfde waarde TRUE. Hetzelfde gebeurt als je een van de drie naar FALSE vouwt (10 en 11).

11 - Als je één input naar rechts draait, draaien        de twee outputs ook naar rechts	12 - De intersector laat je toe om twee lijnen te kruisen

Wanneer je in de praktijk complexe schakelingen zou construeren, zou je misschien op een bepaald moment ontdekken dat je in de problemen komt omdat je lijnen wilt kruisen. En dan liggen alle signalen niet meer in één vlak, want dan moet één lijn over een andere gaan.

Maar ook hiervoor hebben de wiskundigen een oplossing: ze creëerden intersectors. Hierdoor gaat één lijn schuin en één horizontaal. Beide lijnen kun je van waarde (TRUE of FALSE) veranderen zonder dat dit een invloed heeft op de waarde van de andere. Verder hebben ze ook een component uitgevonden die lijnen die te veel zijn (bijvoorbeeld output van de zeshoekige of driehoekige draai) te absorberen. Die component heet de eater (12).

Turingvolledig

Uiteindelijk hebben Hull en Zakharevich ook bewezen dat hun origamiconstructies turingvolledig zijn. Dat betekent dat ze even krachtig zijn als een universele turingmachine, en dus alle mogelijke berekeningen kunnen uitvoeren. Om dat te bewijzen, hebben ze met hun origamipoorten een vouwpatroon gecreëerd dat de cellulaire automaat Regel 110 (https://mathworld.wolfram.com/Rule110.html) simuleert. Hiervan heeft Matthew Cook in 2004 bewezen dat die turingvolledig is, en daardoor weten we nu ook dat vlak gevouwen origami turingvolledig is (12).

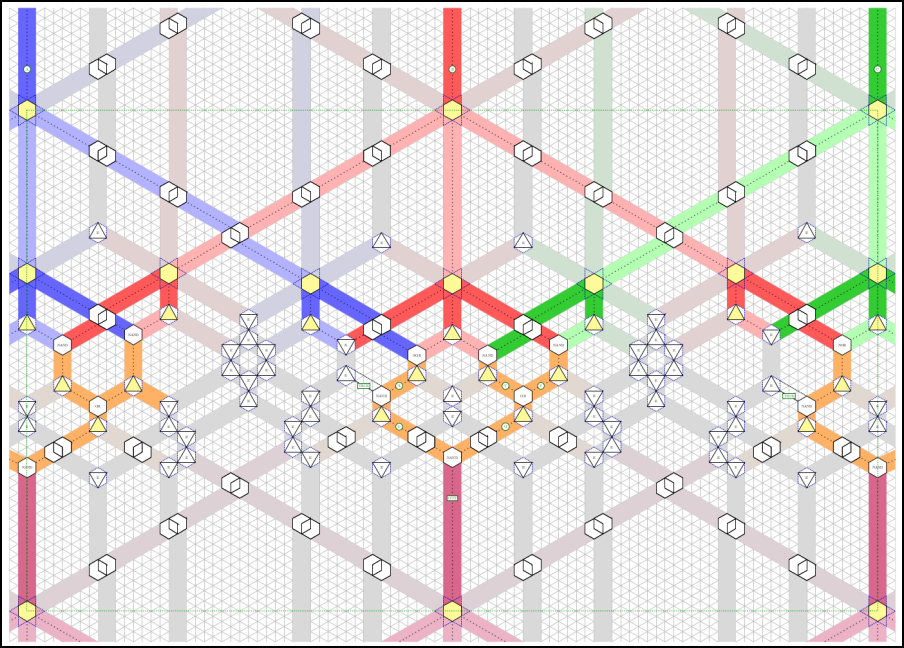Het vouwpatroon dat de cellulaire automaat Regel 110 simuleert

Deze Regel 110 effectief op deze manier vouwen zou een gigantische taak zijn, zelfs voor origamimeesters. En hier dan ook nog eens de berekeningen mee uitvoeren door de inputs te vouwen en dan de bits door alle poorten heen vouwen helemaal tot de outputs, zou heel onpraktisch zijn. Wat Hull en Zakharevich bewezen hebben, heeft dus geen enkel praktisch nut. Maar het doet wel nadenken over de essentie van computers. Die hoeven in principe helemaal niet op elektronische manier te werken. Dat zelfs het vouwen van een eenvoudig blad papier voldoende is om berekeningen uit te voeren, is een diepe gedachte.