In deze derde en laatste aflevering over Sudoku’s laat ik zien dat veel van de 33 patronen waaronder de X-wing een krachtig stukje logica verbergen. Wie dat doorheeft, kan al die patronen vergeten!

Henk van de Kamer
In de vorige aflevering maakte ik een Python-programma die met menselijke logica in code driehonderd moeilijke Sudoku’s oplost. Uiteindelijk bleek het zoeken naar naked (S) en hidden singles (A) plus pointing numbers (B) afdoende. De tip in de eerste aflevering vindt ook naked pairs, maar die zijn blijkbaar niet essentieel.
SABC set
Met de gecombineerde SAB-methode zijn 2.163 Sudoku’s in een door mij gemaakte set van twintigduizend stuks nog niet opgelost. Als ik in deze naked pairs (C) gebruik, worden er nog eens 162 opgelost. Een deel van deze set heb ik ondertussen zelf opgelost via de tipmethode en ongeveer de helft gaat soepel.
In de andere helft wordt ‘het naakte paartje’ niet gevonden en moeten we deze via tellen opsporen in cellen die al veel nummers zien. Sommige kosten mij meer dan een uur, ofwel zo bekeken heb ik het doel waarmee ik de eerste aflevering begon al gehaald. Namelijk Sudoku’s vinden die ondanks de tip nog steeds niet makkelijk oplosbaar zijn. Wie interesse heeft in deze set kan mij een mailtje sturen. Het is een XML-bestand die geïmporteerd kan worden in de Open Sudoku-app. Of je opent dit bestand en kopieert de strings die de Sudoku coderen in een app van jouw keuze.
X-wing
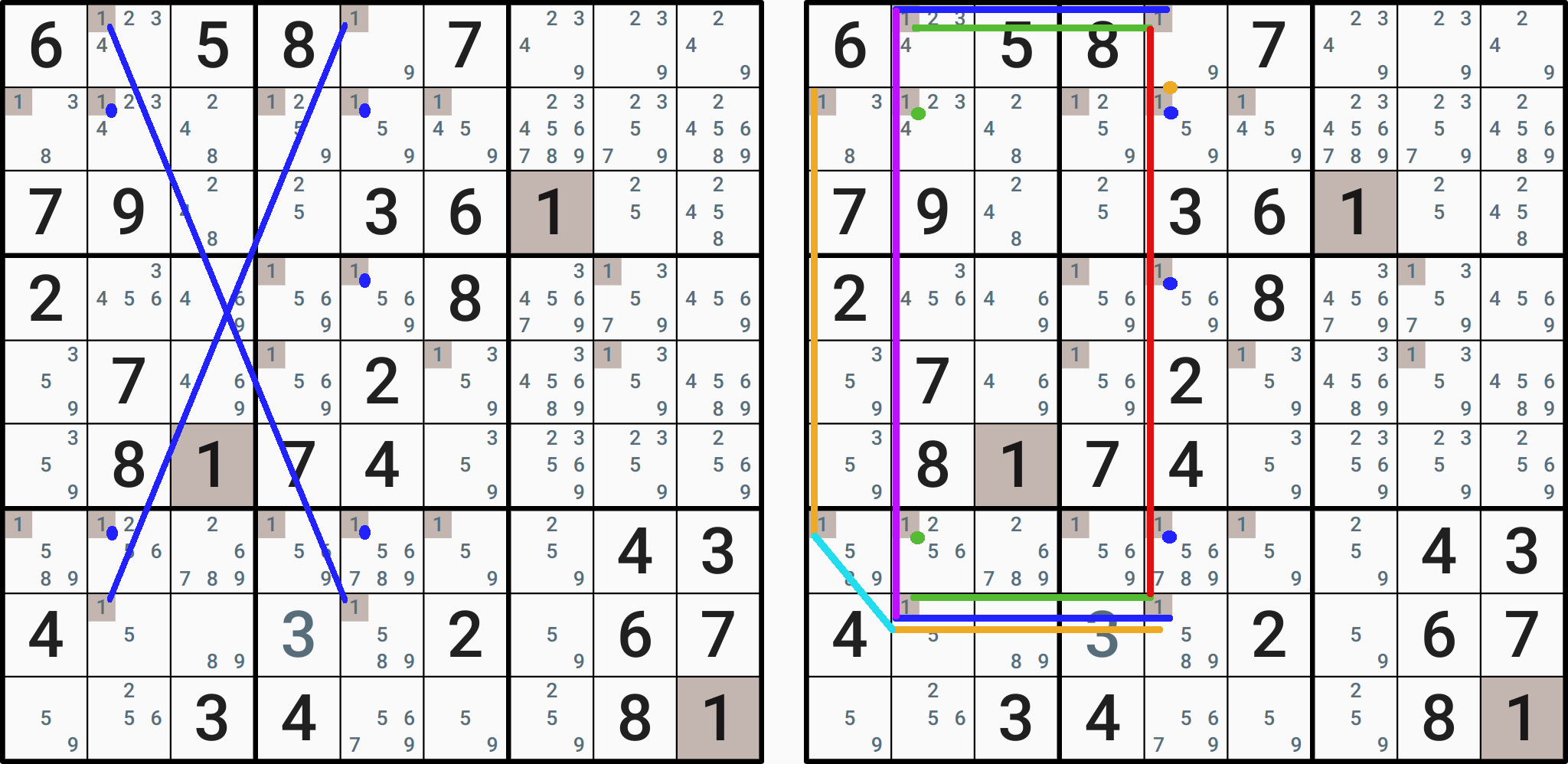
De SABC-set bevat nog steeds niet het X-wing-patroon waar de zoektocht mee begon. Links in de afbeelding zie je een screenshot – via https://sudoku.simonton.app/ gemaakt – van een Sudoku waarin een tweetal X-wings aanwezig zijn. De eerste is via het cijfer 6, maar deze is gemakkelijker te herkennen als pointing number. De andere ontstaat na het invullen van een 3 in de achtste rij, vierde kolom. In deze cel waren de cijfers 1, 3, 5 en 9 nog mogelijk volgens de boekhouding. De 3 is echter een hidden single. Na invullen verdwijnt de 1 en ontstaat de in blauw weergegeven X-wing met dit cijfer.
 |
|
Het X-wing patroon en de onderliggende logica via kettingen |
Het oplossen van een Sudoku komt vaak neer op het herkennen van een rij, kolom of vierkant waarin een cijfer nog maar op één of twee plaatsen ingevuld kan worden. De tip ontdekt veel, maar niet alle situaties zoals de gevonden SABC-set al liet zien. In de eerste en achtste rij kan de 1 nog maar op twee plaatsen. Op zich niet bijzonder nuttig, behalve dat het ook nog eens dezelfde twee kolommen zijn! Nogmaals voor alle duidelijkheid: een X-wing bevat in twee rijen of kolommen nog maar twee mogelijke plaatsen voor respectievelijk de kolom of rij. En die moet voor beide dezelfde zijn, ofwel de vier cijfers vormen de hoekpunten van een rechthoek.
Logica
Logica is een tak van de wiskunde en zoals gezegd is dat de reden waarom Sudoku’s mij aanspreken. In de getoonde X-wing kun je in een willekeurig hoekpunt beginnen met de volgende redenatie. Stel dat in r8k2 – afkorting voor de cel in rij 8, kolom 2 – het cijfer 1 de uiteindelijke oplossing is. In dat geval moet in r8k5 één van de andere cijfers de oplossing zijn. Waarmee de uiteindelijke oplossing in r1k5 het cijfer 1 geplaatst moet worden en in r1k2 één van de andere nog mogelijke cijfers. Als je deze ketting begint met een 1 in bijvoorbeeld r1k2, dan moet in r8k5 eveneens een 1 geplaatst worden. Dat verklaard de naam X-wing.
Welke van beide mogelijke kettingen uiteindelijk juist blijkt, is net zoals met paartjes op dit punt in het oplossen niet van belang. Wat we met logica bewezen hebben, is dat alle andere plaatsen voor de 1 in kolom twee en vijf niet mogelijk zijn. We kunnen dus vijf enen – aangegeven met een blauwe punt – in de boekhouding verwijderen.
Ketting
Zoals in de eerste aflevering in deze serie gezegd, was het X-wing-patroon mij duidelijk. Maar tijdens het programmeren vroeg ik mij af waarom het een rechthoek zou moeten zijn. Na een zoektocht ontdekte ik een uitleg waar veel van de 33 patronen als een ketting met sterke en zwakke schakels werden getekend. Een sterke schakel is een lijn tussen exact twee mogelijke posities in een rij, kolom of vierkant. Een zwakke schakel is een verbinding tussen twee sterke schakels. Dit mag ook een sterke schakel zijn, maar in de ketting beschouwen we de even schakels als zwak.
In bovenstaande X-wing is r1k2 naar r1k5 (of andersom) een sterke schakel, weergegeven als groene lijn in het middelste deel van de afbeelding. Vergeet even de andere gekleurde lijnen, daar kom ik straks op terug. Ook r8k5 naar r8k2 is een sterke schakel. Vervolgens kijken we of twee eindpunten van sterke schakels – zie bijvoorbeeld ook de verticale oranje versie in de eerste kolom – in dezelfde rij, kolom of vierkant aanwezig zijn. Zo ja, dan mogen we daar een zwakke of als zwak aangeduide sterke schakel tekenen. De r1k5 naar r8k5 en r7k1 naar r8k2 zijn dus mogelijke zwakke schakels omdat in respectievelijk de kolom en vierkant meer dan twee posities voor het cijfer 1 beschikbaar zijn.
Een ketting heeft altijd een oneven aantal schakels. De oneven schakels in deze ketting moeten sterk zijn. De even maakt zoals gezegd niet uit, zolang ze getekend worden in dezelfde kolom, rij of vierkant. In de figuur zijn drie van de vier mogelijke kettingen met drie schakels getekend. De groen-rood-groen en blauw-paars-blauw vormen de rechthoek van het X-wing-patroon. Na het maken van de ketting controleren we of de eindpunten dezelfde cel zien via een kolom, rij of vierkant. Zo ja, dan kan het cijfer dat voor de ketting is gebruikt, in die cel worden verwijderd in de boekhouding.
Je ziet dat de derde – en niet getekende vierde ketting – een deel van de boekhouding aanpassen die de X-wing al heeft gedaan. Stel echter dat in de eerste rij drie of meer enen aanwezig waren. Dan had de oranje-lichtblauw-oranje ketting nog steeds gewerkt. De enkele schakel van r4k8 naar r5k8 heeft geen mogelijke zwakke schakel naar één van de andere sterke schakels.
AIC type 1
De getoonde kettingen heten op zijn Engels Alternate Inference Chain. Grofweg vertaald ‘afwisselende gevolgtrekking ketting’. De gevolgtrekking hint naar slechts twee locaties voor een cijfer in een rij, kolom of vierkant. Dus als we via andere aanwijzingen een van beide als waar ontdekken, moet de andere automatisch onwaar zijn. En visa versa. Het afwisselende is combineren van sterke schakels via zwakke waarin geen gevolgtrekking mogelijk is.
Als beide eindpunten eindigen op hetzelfde cijfer, noemen we het type 1. Waarmee duidelijk is dat er ook kettingen bestaan die op een ander cijfer eindigen. Hoe dat werkt, ga ik in de toekomst bestuderen, want deze logica begrijpen is een stuk lastiger. De kleinste ketting heeft drie schakels, maar kettingen met vijf, zeven of meer oneven schakels zijn ook mogelijk. Deze zijn echter moeilijker te vinden. Mijn volgende set Sudoku’s gaan dus niet de X-wing bevatten, maar versies waarin een AIC type 1 en lengte drie zorgen voor een doorbraak in het opschonen van de boekhouding met als eindresultaat een oplossing.
Tot slot
Ik leer door zelf te experimenteren met zaken die ik lees of hoor. De rest zijn woorden die worden opgeslagen, maar waar ik niets mee kan. De gemakkelijke en gemiddelde Sudoku’s vormden al snel geen uitdaging meer. Via de harde Sudoku’s leerde ik als eerste de boekhouding-truc. Dat lijkt krachtig, maar als snel was duidelijk dat het niets meer is dan een onderdeel in de oplos-gereedschapskist. Verder beschouwde ik het ook als valsspelen, maar dat is onzin. Zonder boekhouding zijn zeer moeilijke Sudoku’s niet op te lossen. Dankzij de tip kan ik het gebruik van de boekhouding uitstellen, maar ook deze heeft zijn beperkingen.
In een ver verleden heb ik over de kettingen gelezen, maar had ik geen Sudoku’s waarin deze nodig waren. De afgelopen drie afleveringen maken duidelijk dat dit pas voor de volgende fase nodig is. En al die patronen hoef ik niet te leren. Dat is net zo onzinnig als het leren van jaartallen in geschiedenis, tafels voor het rekenen of plaatsnamen in de aardrijkskunde. Zoals gezegd is dat niet mijn manier waarop ik dingen leer.
Daarmee sluit ik het onderwerp Sudoku’s af. Mochten zaken niet duidelijk zijn, schroom dan niet om met mij te mailen!


